Experimental Setup
The experimental setup for two-phototn photoemission can be divided into two parts:
- outside the vacuum chamber: the optical setup which is used to generate the two light pulses
- inside the vacuum chamber: the sample and the energy analyzer
Optics
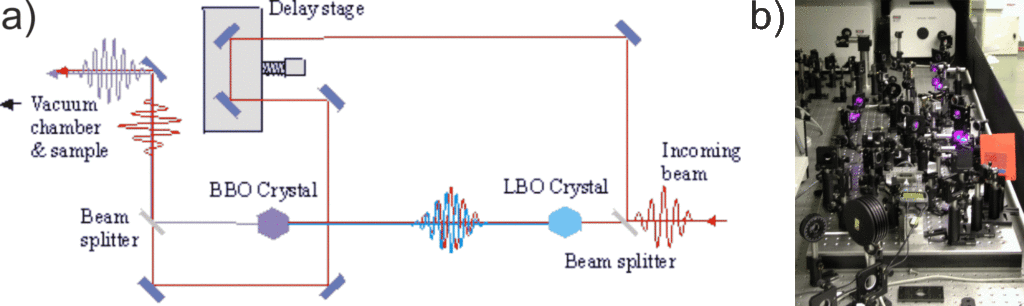
The basic instrument to generate short pulses is the femtosecond laser. The principles of this type of laser are explained in the previous chapter. However in two-photon photoemission two laser pulses are used. The energy of this second beam has to be adjusted to the experiment. If you want photons with the same energy, which is the easiest case, you will just have to split the basic beam into two. Usually, a pulse with double or triple frequency is chosen.
In a tripler the beam is split into two. One is directly used as the probing pulse. The other beam traverses a LBO crystal and a certain percentage is transformed to a beam with double frequency. This beam is split from the origin beam and compressed in time with two prisms. Then this beam is added to the original beam via a BBO crystal. The resulting 3hv beam is compressed again with two prisms. The probe 1hv beam traverses a delay stage. Thus the time difference between these beams can be varied.
Detection

After passing a quartz window at the vacuum chamber the photons hit the sample and produce photoelectrons. Their energy can be detected. There are several types of analyzers. We will just have a short look on the hemispherical analyzer . After passing a lense system, the electrons enter an electric field formed by two hemispheres with a potential difference U. The field is given by
E(r) = \frac{U}{r^2}\frac{ab}{b-a}whereby b and a are the radii of the two hemispheres. Assuming that both, the entrance slit and the detector lie opposite between the two hemispheres at a radius of
r = \frac{b-a}{2}only electrons with an energy of
E = \frac{eU}{b/a-a/b}can reach the detector and cause a signal. By varying the potential difference the energy is scanned and a spectrum is obtained.